Сабақ жоспары (ұмж): Центрлік және іштей сызылған бұрыштар 2-сабақ (Геометрия, 9 сынып, IV тоқсан)

Пән: Геометрия
Ұзақ мерзімді жоспар бөлімі: Шеңбермен байланысты бұрыштар
Сабақ тақырыбы: Центрлік және іштей сызылған бұрыштар 2-сабақ
Оқыту мақсаты: центрлік және іштей сызылған бұрыштар ұғымдарын біледі;
9.3.2.4 іштей сызылған бұрыш туралы теореманы және оның салдарын дәлелдейді және қолданады
Сабақ мақсаты: центрлік және іштей сызылған бұрыштар ұғымдарын біледі; іштей сызылған бұрыш туралы теореманы және оның салдарын дәлелдейді және қолданады.

Ұйымдастыру кезеңі
Жұптық жұмыс:
Оқушылар өткен материал бойынша бір-біріне сұрақтар қояды.
Шеңбер дегеніміз не?
Радиус дегеніміз не?
Диаметр дегеніміз не?
Хорда дегеніміз не?
Жанама дегеніміз не?


Жаңа тақырыпты түсіндіру.
Проблемалық жағдаят: АОВ және АСВ бұрыштарының ұқсастығы мен айырмашылығы неде?

Сабақтың тақырыбы мен мақсаттарын айқындау.
Анықтама. Төбесі шеңбердің центрінде жататын бұрыш центрлік бұрыш деп аталады. Бұрыштың ішінде орналасқан шеңбер бөлігі осы центрлік бұрышқа сәйкес шеңбер доғасы деп аталады.

АКВ доғасы АОВ центрлік бұрышына сәйкес. Шеңбер доғасының градустық өлшемі деп оған сәйкес центрлік бұрыштың градустық өлшемін атайды.

Анықтама.Төбесі шеңберде жататын, ал қабырғалары сол шеңберді қиып өтетін бұрыш шеңберге іштей сызылған бұрыш деп аталады.
АВС бұрышы шеңберге іштей сызылған . Оның В төбесі шеңбер бойында жатыр, ал бұрыштың қабырғалары шеңберді А және С нүктелерінде қиып өтеді. А және С нүктелері шеңберді екі доғаға бөледі. В нүктесі жатпайтын доғаға сәйкес центрлік бұрыш іштей сызылған В бұрышына сәйкес центрлік бұрыш деп аталады. Сонымен шеңберге іштей сызылған АВС бұрышына сәйкес центрлік бұрыш АОС бұрышы болады.


Теорема: Шеңберге іштей сызылған бұрыш өзіне сәйкес центрлік бұрыштың жартысына тең болады.
Теореманы дәлелдеу үшін 3 жағдайды қарастырамыз:
1. Бұрыштың бір қабырғасы шеңбердің центрінен өтеді. АО радиусын жүргізсек, теңбүйірлі АВО үшбұрышы шығады, мұнда АО=ОВ, сондықтан . 2∙∟АВО=∟AOD AOD бұрышы АВО бұрышына қатысты сыртқы бұрыш, сондықтан ол АВО және ВАО бұрыштарының қосындысына тең, яғни екі еселенген АВО бұрышына тең: . Осы себепті АВО бұрышы AOD центрлік бұрышының жартысына тең: .
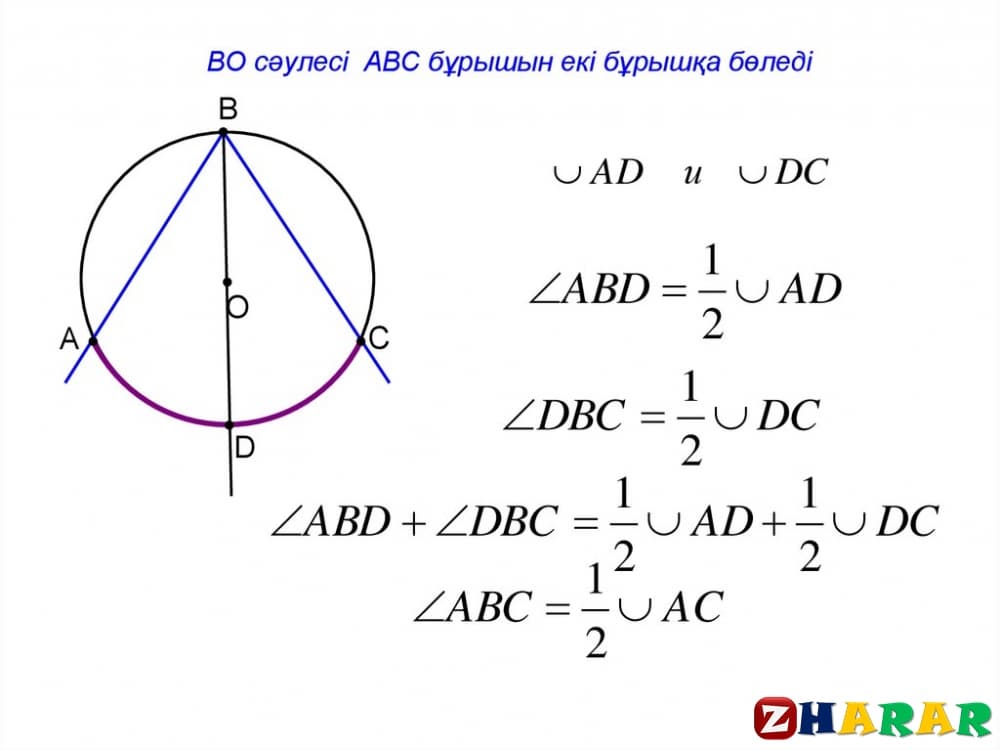
2. Шеңбердің О центрі шеңберге іштей сызылған бұрыш қабырғаларының арасында жатады. ВD диаметрін жүргіземіз, сонда
.
3. Шеңбердің О центрі шеңберге іштей сызылған АВС бұрышынан тысқары жатсын. ВD диаметрін жүргіземіз, сонда .
Теорема дәлелденді.......